Aplicaciones I

Modelo Insumo-Producto

Aplicación tomada del libro "Matemática para Economistas con Excel y Matlab" de Alicia Bernardello y coautores

Características del modelo:

Describe relaciones interindustriales o intersectoriales.
Usa dichas relaciones para predecir cambios en la demanda para predecir causados por cambios en la demanda autónoma del los productos finales.

Suponga una economía con tres sectores:

Prod/Ins	I	II	III
I	0.2	0.6	0
II	0.2	0	0.2
III	0.4	0.2	0.5

Columna 1: Por cada peso producido del producto I se usan: 0.2 pesos del mismo producto, 0.2 pesos del producto II, y 0.4 pesos del producto III.
La demanda de cada una de las tres industrias está compuesta de la demanda derivada de las otras industrias y la demanda autónoma:

\begin{eqnarray} x_1 &=& 0.2x_1+0.6x_2+d_1 \ x_2 &=& 0.2x_1+0.2x_3+d_2 \ x_3 &=& 0.4x_1+0.2x_2+0.5x_3+d_3 \ \end{eqnarray}

Definamos la matriz de coeficientes técnicos como:

clear all;
A = [0.2 0.6 0; 0.2 0 0.2; 0.4 0.2 0.5]

A =

    0.2000    0.6000         0
    0.2000         0    0.2000
    0.4000    0.2000    0.5000

Si definimos los vectores $x=(x_1,x_2,x_3)'$ y $d=(d_1,d_2,d_3)'$ tenemos:

$$x = Ax + d$$

Entonces:

$$x=(I-A)^{-1}d$$

La matriz $I-A$ es denominada matriz de Leontief.
La matriz $A$ tiene todo sus autovalores en el círculo unitario y $I-A$ es no singular. Entonces $(I-A)^{-1}$ es no negativa.

eigA = eig(A)
detL = det(eye(3)-A)

eigA =

    0.7445
    0.1432
   -0.1877


detL =

    0.2600

invL = inv(eye(3)-A)

invL =

    1.7692    1.1538    0.4615
    0.6923    1.5385    0.6154
    1.6923    1.5385    2.6154

Si $d_1=100$, $d_2=50$, y $d_3=200$, las demandas sectoriales serían:

d = [100; 50; 200]
x = invL*d

Nos interesa calcular el efecto de un cambio en la demanda autónoma de un producto sobre la demanda total (dadas las relaciones entre sectores).

$$\Delta x = (I-A)^{-1} \Delta d$$

Suponga ahora $d'_1=110$, $d'_2=100$, y $d'_3=180$.

d2 = [110; 100; 180];
Dd = d2-d
Dx = invL*Dd

Equilibrio de Mercado con Dos Bienes

Aplicación tomada del libro "Matemática para Economistas con Excel y Matlab" de Alicia Bernardello y coautores

El Modelo:

Función de Demanda del producto 1: $$Q_{d1} = 40 - 2 P_1 + P_2$$
Función de Oferta del producto 1: $$Q_{o1} = -5 + 3 P_1 - P_2$$
Equilibrio en el mercado 1: $$Q_{d1}=Q_{o1}=Q_1$$
Función de Demanda del producto 2: $$Q_{d2} = 90 + P_1 - P_2$$
Función de Oferta del producto 2: $$Q_{o2} = -2 + 2 P_2 $$
Equilibrio en el mercado 2: $$Q_{d2}=Q_{o2}=Q_2$$

El modelo puede ser resuelto usando el método de reemplazo para encontrar la solución al sistema de ecuaciones. Bastante tedioso. Definamos mas bien el siguiente vector: $$x = (Q_1,Q_2,P_1,P_2)'$$

Definamos entonces: $$ Ax = b$$

La solución del sistema de ecuaciones es entonces (si $A$ es invertible): $$x = A^{-1} \times b$$

A = [1 0 2 -1;
     1 0 -3 1;
     0 1 -1 1;
     0 1 0 -2]
b = [40; -5; 90; -2]
dA = det(A)

A =

     1     0     2    -1
     1     0    -3     1
     0     1    -1     1
     0     1     0    -2


b =

    40
    -5
    90
    -2


dA =

   -13

Solución:

x = A \ b   % alternativamente x =inv(A)*b

Entonces: $Q_1=29.7$ ,$P_1=24.5$, $Q_2=75.7$, $P_2=38.8$ .

Mínimos Cuadrados Ordinarios

Construiremos dos vectores $X_1$ y $X_2$ de $N \times 1$ cada uno y con ello un vector $y$ de acuerdo a:

$$y_i = 3 + 0.5X_{1i} + 0.9X_{2i} + \epsilon_i$$

donde $X_{1i} \sim N(1,4)$, $X_{2i} \sim N(2,4)$ y $\epsilon \sim N(0,1)$.

A partir de estos datos usaremos la fórmula estándar de MCO para encontrar los coeficientes estimados. $$\hat{\beta} = (X'X)^{-1} X'y$$

Generando Datos:

N = 100;
X1 = 1 + 2*randn(N,1);
X2 = 2 + 2*randn(N,1);
eps = randn(N,1);
y  = 3 + 0.5*X1 +0.9*X2 + eps;

data = [y X1 X2];

dlmwrite('DatosMCO.txt',data);

Cargando Datos y estimado los parámetros:

clear all;
whos

impdata = importdata('DatosMCO.txt');
whos;

Name           Size            Bytes  Class     Attributes

  impdata      100x3              2400  double

[N, K] = size(impdata);
y = impdata(:,1);
X1 = impdata(:,2);
X2 = impdata(:,3);

X = [ones(N,1) X1 X2];

beta = (X'*X)\(X'*y)   % alternativa beta = inv(X'*X)*(X'*y)

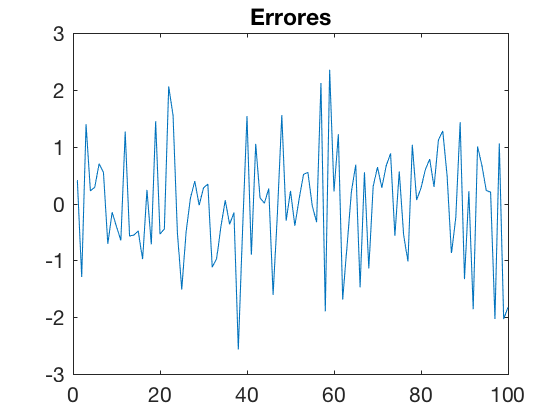
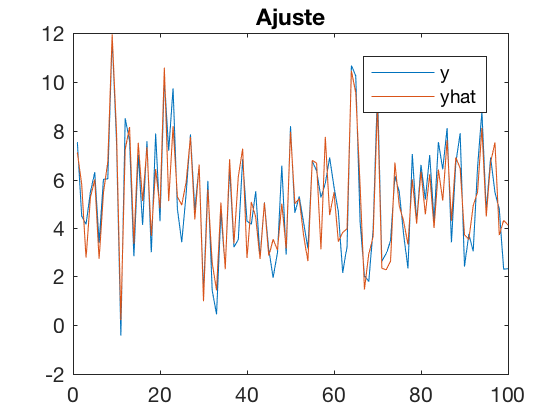
Graficando la predicción y los errores del modelo.

err = y - X*beta;
yhat = X*beta;

plot([y yhat]);
title('Ajuste')
legend('y','yhat');

png

plot(err);
title('Errores');

png