12 Optimización
La exposición en esta sección sigue de cerca el capítulo 4 del libro de Miranda y Fackler.
En esta sección se describe cómo maximizar numéricamente una función respecto de un vector finito de variables. El problema a resolver es entonces:
\[\max_{x \in X} f(x)\]
con \(x \subseteq R^n\). En este problemas denominamos a \(f\) como la función objetivos, a \(X\) como el conjunto factible y a \(x^*\) como el máximo (si existe).
Los problemas de optimización finitos son muy comunes en economía.
*Teorema de Wierstrass**
Si \(f\) es continua y \(X\) es un conjunto no vacío, cerrado y acotado, entonces \(f\) tiene un máximo en \(X\).
Condición de Primer Orden:
\[f'(x^*) = 0\]
12.1 Métodos Numéricos de Optimización: Ideas Básicas
El Método de Newton-Rapson
El método de Newton-Rapson usa una sucesión de aproximaciones cuadráticas de la función objetivo y el máximo de la aproximación debería converger al máximo de la función.
Este método está estrechamente relacionado con el método de Newton para buscar las raíces de una función.
El método es iterativo y se inicia con una conjetura \(x^{(0)}\) de la solución.
A continuación se actualiza la solución de \(x^{(k)}\) a \(x^{(k+1)}\) minimizando:
\[f(x) \approx f(x^{(k)}) + f'(x^{(k)})(x-x^{(k)}) + 0.5 (x-x^{(k)})^{T}f''(x^{(k)})(x-x^{(k)})\]
respecto de \(x\). La condición de primero orden es:
\[f'(x^{(k)}) + f''(x^{(k)})(x-x^{(k)})=0\]
y por tanto:
\[x^{(k+1)} \leftarrow x^{(k)} - [f''(x^{(k)})]^{-1} f'(x^{(k)})\]
El algoritmo termina cuando \(x^{(k+1)}\) es suficientemente cercano a \(x^{(k)}\).
Limitaciones: - Se requiere computar tanto la primera como la segunda derivadas de la función (el gradiente y la matriz hessiana). - No hay garantía que la función se incremente en la dirección de la actualización (esto se garantiza sólo si \(f''\) es definida negativa). - EL método de Newton-Rapson es usada sólo cuando la función es globalmente cóncava.
El Método de Quasi-Newton
Sigue la misma idea que el método de Newton-Rapson pero reemplaza la matriz hessiana con una aproximación que es definida negativa (garantizando incrementos en la función).
Por eficiencia, la aproximación se realiza directamente sobre la inversa de la matriz hessiana. El método Broyden-Fletcher-Goldfarb-Shano (BFGS) satisface esta idea.
El Método Nelder-Mead
El objetivo es encontrar el simplex que contiene el punto que minimiza (localmente) la función. Este método no requiere derivadas y va buscando el mínimo iterativamente mediante un proceso de reemplazo de puntos. Si el problema es minimizar una función \(f(x): R^N \rightarrow R\) entonces el simplex tendrá \(n+1\) vértices. El método evaluará la función en cada uno de estos \(n+1\) vértices y reemplazará el peor valor de la función por una nueva conjetura. Este proceso se realiza en 4 pasos que son denominados (1) reflejo, (2) expansión, (3) contracción, y (4) encoger. Por ejemplo, si suponemos que buscamos el mínimo de la función \(f(x): R^2 \rightarrow R\), entonces el simplex tendrá 3 vértices (un triángulo) y en cada paso de la iteración se reemplazará el peor valor de la función por un nuevo vértice del triángulo. Este proceso mueve el triángulo siempre hacia abajo en dirección de la función. Los siguientes diagramas disponibles en Wikipedia muestran gráficamente este proceso:
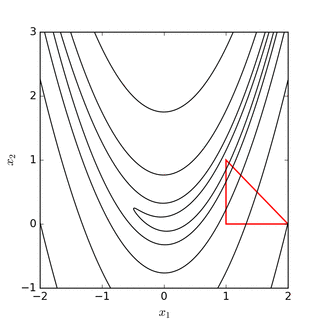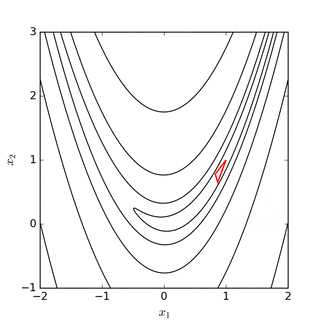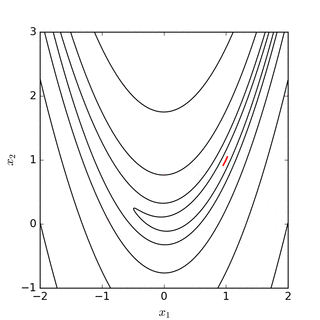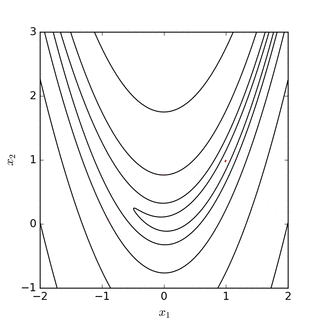
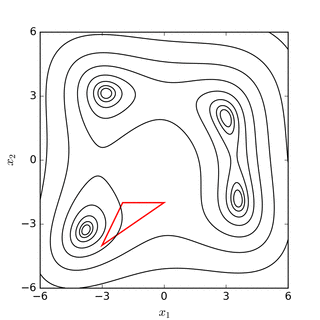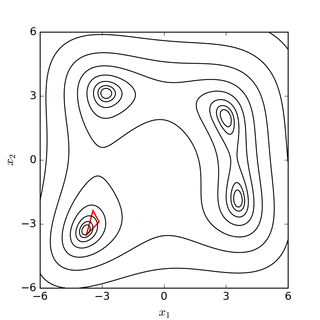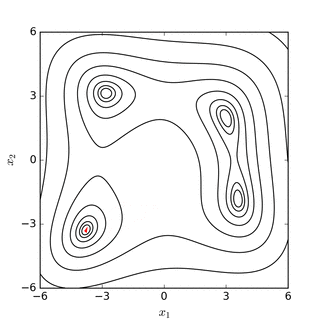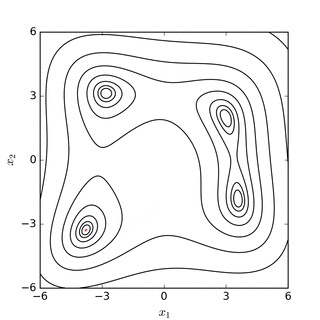
Fuente: Wikipedia
Este es un método bien popular cuando las derivadas no son bien comportadas y es relativamente rápido (aunque en general requiere de un gran número de evaluaciones de la función).
12.2 Paquetes de Optimización de Julia (Optim y JuMP)
El paquete Optim implementa varios procedimientos de optimización. En particular, el paquete busca \(x\) en \(R^n\) de tal manera de minimizar la función \(f(x):R^n \rightarrow R\). El paquete incluye procedimientos de optimización como los descritos antes y se centra principalmente en problemas no restringidos. Optim tiene algún soporte para optimización restringida, pero este es únicamente para restricciones en los límites de las variables de elección.
Nota: Optim tiene implementados los métodos numéricos anteriores con el objetivo de minimizar una función. La maximización se realiza simplemente minimizando el negativo de la función objetivos.
Minimización No Restringida usando Optim
Julia minimiza funciones no lineales sin restricciones usando la función optimize().
La función busca iterativamente el mínimo de una función escalar con varias variables a partir de una conjetura inicial.
La sintaxis general es:
resultado = optimize(fun, gfun, hfun, x0, método, otras_opciones)
Los inputs de la función son:
fun: Función escalar objetivo.gfun: Gradiente (opcional)hfun: Matriz Hessiana (opcional)x0: Conjetura inicial.métodos: Método de optimización (entre otros Newton, BFGS, Nelder Mead).otras_opciones: opciones de optimización (número de iteraciones, tolerancia, mostrar iteraciones, entre otros)
El método de optimización a usarse depende del problema. Si el gradiente gfun y la hessiana hfun están disponibles se usa el método de Newton(). Si el el gradiente y la hessiana no está disponibles, los métodos de Quasi-Newton son usados: BFGS() o LBFGS(). Finalmente, si la función no es diferenciable se usa el método de Nelder-Mead().
Los resultados de interés se encuentran en:
resultado.minimizer: \(x^*\) que minimiza la función.resultado.minimum: función evaluada en el óptimo \(f(x^*)\).
Resolvamos el siguiente ejemplo:
\[f(x)=3x^2_1 +2x_1 x_2 +x^2_2 -4x_1 + 5x_2\]
Escribamos la función anónima.
funx (generic function with 1 method)Para hallar el mínimo partimos de la conjetura \([1,1]\).
2-element Array{Float64,1}:
2.2499999999837983
-4.749999999964962 -16.375Para aproximar las derivadas optimize() usa por defecto el método de diferencia finitas. No obstante, es posible usar alternativamente Diferenciación Automática, para ello se usa la opción autodiff = :forward:
2-element Array{Float64,1}:
2.25
-4.75Algunas de las opciones se declaran bajo Optim.Options() y las más utilizadas son:
x_tol: Tolerancia relativa a cambios en el vector x (por defecto 0.0).f_tol: Tolerancia relativa a cambios en la función objetivo (por defecto 0.0).f_calls_limit: Número máximo de evaluaciones de la función. (por defecto 0, que significa ilimitado).iterations: Máximo número de iteraciones (por defecto 1000).show_trace: Mostrar resultados de iteraciones (por defecto false).
Usemos ahora el método de Nelder Mead (Simplex) mostrando las iteraciones y restringiendo a que el máximo número de iteraciones sea 50:
res_min = optimize(funx, x0, NelderMead(), Optim.Options(show_trace = true, iterations = 50));
res_min.minimizerIter Function value √(Σ(yᵢ-ȳ)²)/n
------ -------------- --------------
0 7.000000e+00 2.051376e+00
1 7.000000e+00 3.268771e+00
2 2.009219e+00 4.721712e+00
3 -4.531133e+00 5.965001e+00
4 -1.257614e+01 4.552313e+00
5 -1.524052e+01 1.250000e+00
6 -1.524052e+01 3.248085e-01
7 -1.591637e+01 4.124580e-01
8 -1.622880e+01 1.601745e-01
9 -1.627810e+01 2.038907e-02
10 -1.627810e+01 3.624890e-02
11 -1.634458e+01 3.331949e-02
12 -1.635235e+01 8.676904e-03
13 -1.636560e+01 6.088693e-03
14 -1.636560e+01 2.835991e-04
15 -1.636560e+01 4.211148e-03
16 -1.637430e+01 4.048255e-03
17 -1.637430e+01 3.466096e-03
18 -1.637430e+01 1.526553e-03
19 -1.637430e+01 8.710935e-04
20 -1.637430e+01 5.071956e-04
21 -1.637430e+01 5.770953e-04
22 -1.637477e+01 2.000483e-04
23 -1.637477e+01 8.453215e-05
24 -1.637485e+01 6.297472e-05
25 -1.637492e+01 5.722893e-05
26 -1.637499e+01 2.701253e-05
27 -1.637499e+01 1.711999e-05
28 -1.637499e+01 5.082894e-06
29 -1.637500e+01 3.122085e-06
30 -1.637500e+01 1.177134e-06
31 -1.637500e+01 1.402858e-06
32 -1.637500e+01 6.690414e-07
33 -1.637500e+01 1.975975e-07
34 -1.637500e+01 1.333604e-07
35 -1.637500e+01 6.865298e-08
36 -1.637500e+01 2.305463e-08
37 -1.637500e+01 1.510244e-08
38 -1.637500e+01 1.564809e-08
39 -1.637500e+01 1.317066e-09
2-element Array{Float64,1}:
2.250005459308121
-4.750017444233452Para usar el método de Newton es necesario proveer explícitamente el gradiente y la hessiana de la función. En el caso de la función que tomamos como ejemplo tenemos:
- El gradiente es:
\[\left(\frac{\partial f(x_1,x_2)}{\partial x_1}, \frac{\partial f(x_1,x_2)}{\partial x_2}\right) = \left(6 x_1+2x_2−4, 2x_1+2x_2+5 \right) \]
- La Hessiana es: \[ \left(\begin{array}{cc} \frac{\partial^{2}f(x_{1},x_{2})}{\partial x_{1}\partial x_{\text{1}}} & \frac{\partial^{2}f(x_{1},x_{2})}{\partial x_{1}\partial x_{2}}\\ \frac{\partial^{2}f(x_{1},x_{2})}{\partial x_{2}\partial x_{1}} & \frac{\partial^{2}f(x_{1},x_{2})}{\partial x_{2}\partial x_{2}} \end{array}\right)=\left(\begin{array}{cc} 6 & 2 \\ 2 & 2\\ \end{array}\right) \]
Creamos dos funciones:
function gfunx(x)
g = zeros(2)
g[1] = 6*x[1] + 2*x[2] - 4
g[2] = 2*x[1] + 2*x[2] + 5
return g
end
function hfunx(x)
h = zeros(2,2)
h[1,1] = 6
h[1,2] = 2
h[2,1] = 2
h[2,2] = 2
return h
endhfunx (generic function with 1 method)2-element Array{Float64,1}:
2.25
-4.75Minimización Restringida usando Optim
Optim permite resolver problemas restringidos simples en donde las restricciones toman la forma de límites para las variables de elección. En particular, permite resolver el siguiente problema:
\[
\min_{x} f(x) \]
s.a
\[ lb \leq x \leq ub \]
donde \(lb\) y \(ub\) son vectores de la misma dimensión que \(x\).
La sintaxis general es:
resultado = optimize(fun, gfun, hfun, lb, ub, x0, Fminbox(método), otras_opciones)
Los nuevos inputs de la función son:
lb: Vector con límites inferiores (-Infes posible).ub: Vector con límites superiores (Infes posible).Fminbox(): Declara optimización restringida.
Ahora resolvamos el siguiente problema:
\[ \min_{x_1,x_2} f(x_1,x_2) = 1+\frac{x_1}{(1+x_2)} - 3x_1x_2 + x_2(1+x_1) \] s.a \[ 0 \leq x_1 \leq 1 \] \[ 0 \leq x_2 \leq 2 \]
FunObj (generic function with 1 method)Restricciones:
Optimizamos:
2-element Array{Float64,1}:
0.9999999999999999
1.9999999999999998Optimización usado JuMP
JuMP es un lenguaje de optimización matemática escrito en Julia similar a algunos programas comerciales como GAMS. Entre sus principales características están su facilidad para trasladar un problema matemático en uno computacional y que permite utilizar solver externos (tanto open source como comerciales). De acuerdo a la documentación de JuMP, los solvers que éste soporta incluyen: Artelys Knitro, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, y SCS. Aquí se presenta JuMP usando algunos ejemplos y algunas de sus capacidades básicas, para un tratamiento más profundo ver su documentación.
El problema general es encontrar \(x\) que minimiza la función no lineal objetivo \(f(x)\) (lineal o no lineal) sujeto a restricciones, que pueden ser lineales o no lineales y pueden de igualdad o de desigualdad.
El problema general es:
\[ \min_{x} f(x) \] s.a:
\[ Ax = b \] \[ C(x) = 0 \] \[ AIx \leq bI \] \[ CI(x) = 0 \] \[ lb \leq x \leq ub \]
donde \(A\) y \(AI\) son matrices, \(C(x)\) y \(CI(x)\) son funciones no lineales, \(b\) y \(bI\) son vectores columna. La dimensiones de estos objetos dependen del número de restricciones. Finalmente, \(lb\) y \(ub\) son vectores columnas de la misma dimensión que \(x\).
Las opciones básicas de JuMP para declara un modelo de optimización y resolverlo son:
nombre_modelo = Model(with_optimizer(optimizador)): Declara el modelo (vacío)@variable(nombre_modelo, li <= nombre_variable <= ls, tipo variable): Declara variable con el nombrenombre_variable, las restricciones dada por los límites[li,ls], y el tipo de variable (opciones:Binpara binarias eIntpara enteros).@constraint(nombre_modelo, nombre_restriccion, expresión): Declara restricciones lineales definidas porexpresión, las mismas que pueden ser de igualdad==o desigualdad<=,>=.@NLconstraint(nombre_modelo, nombre_restriccion, expresión): Declara restricciones no lineales definidas porexpresión, las mismas que pueden ser de igualdad==o desigualdad<=,>=.@objective(nombre_modelo, [Min/Max], expresión): Declara la función objetivo lineal.@NLobjective(nombre_modelo, [Min/Max], expresión): Declara la función objetivo no lineal.print(nombre_modelo): Imprime en pantalla el modelo en formato legible para humanos.optimize!(nombre_modelo): Resuelve el modelo declarado.
Como ejemplo resolvamos el siguiente problema de optimización lineal trivial:
\[ \text{min} 2x+3y \] sujeto a: \[ x+y \leq 1 \] \[ x \geq 0.1, y \geq 0.1 \] \[ x,y \in \mathbb{R} \]
Cargamos JuMPy el optimizador (en este caso GLPK):
mod_ejemplo = Model(with_optimizer(GLPK.Optimizer))
@variable(mod_ejemplo, x >= 0.1)
@variable(mod_ejemplo, y >= 0.1)
@constraint(mod_ejemplo, x + y <= 1)
@objective(mod_ejemplo, Min, 2*x + 3*y)
println("El problema de optimización es:")
print(mod_ejemplo)El problema de optimización es:
Min 2 x + 3 y
Subject to
x ≥ 0.1
y ≥ 0.1
x + y ≤ 1.0Resolvemos el modelo:
Los resultados son (usamos las funciones JuMP.objective_value y JuMP.value para obtener la función objetivo y los valores de \(x\) e \(y\) que minimizan la función):
println("Función Objetivo: ", JuMP.objective_value(mod_ejemplo))
println("x = ", JuMP.value(x))
println("y = ", JuMP.value(y))Función Objetivo: 0.5
x = 0.1
y = 0.1JuMP resuelve problema de programación lineal generales del tipo:
\[ \text{min} c^T x \] sujeto a: \[ A x \leq b \] \[ x \geq 0 \] \[ x \in \mathbb{R}^n\]
Un ejemplo de problema de minimización de elección de portafolio minimizando el riesgo:
\[ \text{min} RiesgoTotal = \sum_i \sigma_i x_i \] sujeto a: \[ \sum_i x_i (R_i - R_{min}) \geq 0 \] \[ \sum_i x_i (PV_i - PV_{min}) \geq 0 \] \[ 0 \leq x_i \leq 1 \forall i\] \[ \sum_i x_i = 1\]
Supongamos que obtenemos información bursátil de 7 empresas (riesgo, rentabilidad, y precio):
rentabilidad = [0.01130, 0.02565, 0.00440, 0.00972, 0.01259, 0.00652, 0.00681]
riesgo = [0.07752, 0.06172, 0.10399, 0.08940, 0.06157, 0.09916, 0.06297]
precio = [5.89, 28.03, 11.77, 6.6, 56.05, 70.11, 13.47]
rentabilidadmin = 0 # Rentabilidad mínima
preciomin = 0 # Precio mínimo
n = 7;Declaramos el modelo de la misma forma que antes (la única diferencia es que ahora usamos x[1:7] para declarar las 7 variables de una sola vez y usamos list comprehensions para declarar las restricciones y la función objetivo):
portafolio = Model(with_optimizer(GLPK.Optimizer));
@variable(portafolio, 0 <= x[1:n] <= 1)
@constraint(portafolio, c1, sum(x[1:n]) == 1)
@constraint(portafolio, c2, sum([x[i]*(rentabilidad[i]-rentabilidadmin) for i in 1:n]) >= 0)
@constraint(portafolio, c3, sum([x[i]*(precio[i]-preciomin) for i in 1:n]) >= 0)
@objective(portafolio, Min, sum([riesgo[i]*x[i] for i in 1:n]))
println("El problema de optimización es:")
print(portafolio)El problema de optimización es:
Min 0.07752 x[1] + 0.06172 x[2] + 0.10399 x[3] + 0.0894 x[4] + 0.06157 x[5] + 0.09916 x[6] + 0.06297 x[7]
Subject to
x[1] ≥ 0.0
x[2] ≥ 0.0
x[3] ≥ 0.0
x[4] ≥ 0.0
x[5] ≥ 0.0
x[6] ≥ 0.0
x[7] ≥ 0.0
x[1] ≤ 1.0
x[2] ≤ 1.0
x[3] ≤ 1.0
x[4] ≤ 1.0
x[5] ≤ 1.0
x[6] ≤ 1.0
x[7] ≤ 1.0
x[1] + x[2] + x[3] + x[4] + x[5] + x[6] + x[7] = 1.0
0.0113 x[1] + 0.02565 x[2] + 0.0044 x[3] + 0.00972 x[4] + 0.01259 x[5] + 0.00652 x[6] + 0.00681 x[7] ≥ 0.0
5.89 x[1] + 28.03 x[2] + 11.77 x[3] + 6.6 x[4] + 56.05 x[5] + 70.11 x[6] + 13.47 x[7] ≥ 0.0Resolvemos el modelo:
Los resultados son:
println("Función Objetivo: ", JuMP.objective_value(portafolio))
for i in 1:n
println("x$i = ", JuMP.value(x[i]))
endFunción Objetivo: 0.06157
x1 = 0.0
x2 = 0.0
x3 = 0.0
x4 = 0.0
x5 = 1.0
x6 = 0.0
x7 = 0.0La estrategia óptima entonces consiste en invertir todo en una sola empresa, la número 5.
Ahora resolvamos un modelo no lineal. A modo de ejemplo usamos la función de Rosenbrock como función objetivo y resolvamos el siguiente problema:
\[
\min_{x_1,x_2} f(x_1,x_2) = 100(x_2-x^2_1)^2 + (1-x_1)^2
\]
s.a
\[ x_1 + 2x_2 \leq 1 \]
\[ 2x_1 + x_2= 1 \]
Cargamos ahora un optimizador que sea capaz de resolver problemas no lineales (en este caso Ipopt):
nl_mod_ejemplo = Model(with_optimizer(Ipopt.Optimizer));
@variable(nl_mod_ejemplo, x[1:2])
x0 = [0.5, 0]
A = [1, 2]
b = 1
Aeq = [2, 1]
beq = 1
@constraint(nl_mod_ejemplo, ceq, sum(Aeq.*x) == beq)
@constraint(nl_mod_ejemplo, cineq, sum(A.*x) <= b)
@NLobjective(nl_mod_ejemplo, Min, 100*(x[2]-x[1]^2)^2 + (1-x[1])^2)
println("El problema de optimización es:")
print(nl_mod_ejemplo)El problema de optimización es:
Min 100.0 * (x[2] - x[1] ^ 2.0) ^ 2.0 + (1.0 - x[1]) ^ 2.0
Subject to
2 x[1] + x[2] = 1.0
x[1] + 2 x[2] ≤ 1.0Resolvemos el modelo:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.12.10, running with linear solver mumps.
NOTE: Other linear solvers might be more efficient (see Ipopt documentation).
Number of nonzeros in equality constraint Jacobian...: 2
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 1
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+00 1.07e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 7.0257866e+00 1.11e-16 5.24e+01 -1.0 5.03e-01 - 1.00e+00 1.00e+00h 1
2 3.9411734e-01 0.00e+00 8.90e+00 -1.0 2.42e-01 - 1.00e+00 1.00e+00f 1
3 3.4325787e-01 0.00e+00 6.69e-02 -1.0 2.15e-02 - 1.00e+00 1.00e+00f 1
4 3.4271827e-01 0.00e+00 8.13e-04 -2.5 2.37e-03 - 1.00e+00 1.00e+00f 1
5 3.4271758e-01 1.11e-16 1.04e-06 -3.8 8.47e-05 - 1.00e+00 1.00e+00f 1
6 3.4271757e-01 0.00e+00 1.70e-09 -5.7 3.44e-06 - 1.00e+00 1.00e+00h 1
7 3.4271757e-01 0.00e+00 2.59e-13 -8.6 4.23e-08 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 7
(scaled) (unscaled)
Objective...............: 3.4271757484331294e-01 3.4271757484331294e-01
Dual infeasibility......: 2.5923707624997405e-13 2.5923707624997405e-13
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5062219588631739e-09 2.5062219588631739e-09
Overall NLP error.......: 2.5062219588631739e-09 2.5062219588631739e-09
Number of objective function evaluations = 8
Number of objective gradient evaluations = 8
Number of equality constraint evaluations = 8
Number of inequality constraint evaluations = 8
Number of equality constraint Jacobian evaluations = 1
Number of inequality constraint Jacobian evaluations = 1
Number of Lagrangian Hessian evaluations = 7
Total CPU secs in IPOPT (w/o function evaluations) = 3.413
Total CPU secs in NLP function evaluations = 1.921
EXIT: Optimal Solution Found.La solución es:
println("Función Objetivo: ", JuMP.objective_value(nl_mod_ejemplo))
println("x1 = ", JuMP.value(x[1]))
println("x2 = ", JuMP.value(x[2])) Función Objetivo: 0.34271757484331294
x1 = 0.4149443155076643
x2 = 0.1701113689846714