13 Aplicaciones III

13.1 Linealización de una Función

Calculemos la aproximación de Taylor de primer orden de la función \[f (x, y) = xe^{-x^2-y^2}\] alrededor del punto (1,1), esto es: \[f(x,y) ≈ f(1,1)+fx(1,1)(x−1)+fy(1,1)(y−1)\]

El ejercicio consisten entonces en evaluar la función en el punto de aproximación \(f(1,1)\) y encontrar las derivadas parciales con respecto a \(x\) e \(y\), y evaluarlas también en el punto de aproximación: \(f_x(1,1)\) y \(f_y(1,1)\).

El primer paso es definir la función:

fxy(x) = x[1]*exp(-x[1]^2-x[2]^2)

fxy (generic function with 1 method)

Evaluamos la función en el punto \((1,1)\) y calculamos las derivadas parciales evaluada en ese mismo punto:

using Calculus
using Plots
pyplot()

Plots.PyPlotBackend()

fc = fxy([1, 1])
df = Calculus.gradient(fxy,[1, 1])
fx = df[1]
fy = df[2]

fxyaprox(x) = fc - fx - fy + fx*x[1] + fy*x[2]

fxyaprox (generic function with 1 method)

x=[1.1, 1.1]
fo = fxy(x)
fa = fxyaprox(x)
println("Función Original: $fo")
println("Función Aproximada: $fa")

Función Original: 0.09781377920532494
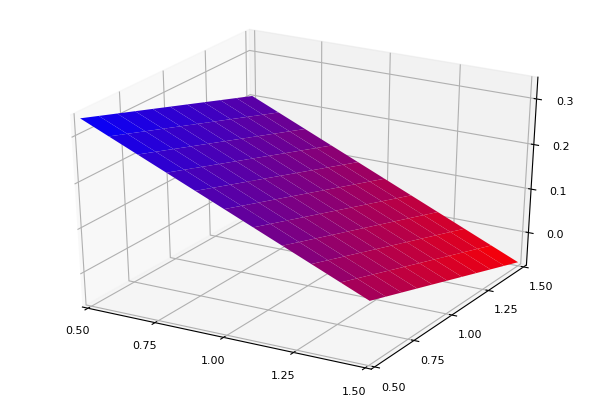
Función Aproximada: 0.09473469826750897

Así luce la aproximación:

x = collect(range(0.5, stop = 1.5, step = 0.1))
n = length(x)

forig = zeros(n,n)
faprox = zeros(n,n)
X = zeros(n,n)

for i in 1:n, j in 1:n
    forig[i,j] = fxy([x[i], x[j]])
    faprox[i,j] = fxyaprox([x[i], x[j]])
    X[i,j] = x[j]
end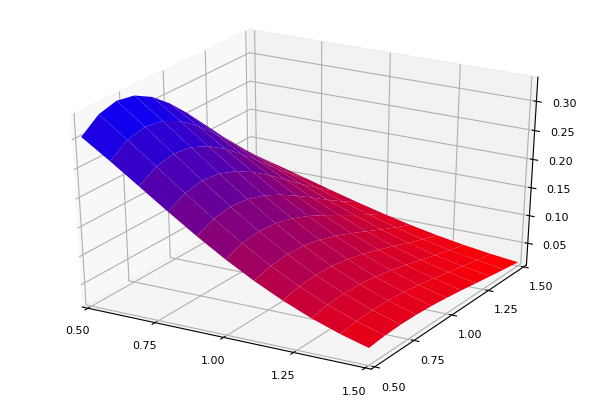

plot(x, x, forig, st=:surface, legend=false, color=cgrad([:red,:blue]), grid = true)

png

plot(x, x, faprox, st=:surface, legend=false, color=cgrad([:red,:blue]), grid = true)

png

13.2 Esperanza Matemática

Calculemos la esperanza matemática de una variable aleatoria normal \(x\): \[E(x) = \int^{\infty}_{-\infty} x f(x)dx\] donde \(f(x)\) es la función de densidad normal. Para esto escribimos la función recordando que:

\[f(x) = \frac{1}{\sigma \sqrt {2\pi}}e^{- \frac{\left( x - \mu \right)^2}{2 \sigma^2} }\]

using QuadGK

function integrando(x,mu,sigma)

    fx = (1/(sigma*sqrt(2*π)))*exp(-(x-mu)^2/(2*sigma^2))
    return x*fx

end

integrando (generic function with 1 method)

integrando_cambiovar(t) = integrando(t/(1-t^2),3,2)*((1+t^2)/(1-t^2)^2)

integrando_cambiovar (generic function with 1 method)

Ex = QuadGK.quadgk(integrando_cambiovar,0,1)

(3.058613587525209, 1.498819803289839e-8)

Alternativamente podemos usar el paquete Distributions que implementa varias distribuciones de probabilidad tanto continuas como discretas. En este ejemplo usaremos la distribución normal y la sintaxis es:

nombre_distribucion = Normal(media, varianza)

Este comando crea un objeto del tipo distribución al cual se le pueden aplicar varias funciones provistas en el paquete. Algunas de estas funciones son:

pdf(nombre_distribucion,x): Función de densidad.
cdf(nombre_distribucion,x): Función de Distribución Acumulada
rand(nombre_distribucion, numero_elementos): Generados de números aleatorios.
quantile(nombre_distribucion, percentiles): Percentiles de la distribución.

La lista de distribuciones que Distributions tiene implementadas y todas las opciones para caracterizar dichas distribuciones puede verse en la documentación.

using Distributions

function integrando2(x,mu,sigma)

    d = Normal(mu, sigma)
    return x*pdf(d,x)

end

integrando2 (generic function with 1 method)

integrando_cambiovar2(t) = integrando2(t/(1-t^2),3,2)*((1+t^2)/(1-t^2)^2)

integrando_cambiovar2 (generic function with 1 method)

Ex = QuadGK.quadgk(integrando_cambiovar2,0,1)

(3.058613587525209, 1.498819803289839e-8)

d = Normal(3, 2)
mean(d)

3.0

13.3 Modelo de Duopolio de Cournot

Aplicación tomada de Miranda y Fackler (2002), Capítulo 3.

Suponga que la demanda de mercado es provista por dos empresas 1 y 2. La función de demanda es:

\[P(q) = q^{1/\eta}\]

con \(q=q_1+q_2\). Laq función de costos de la empresa \(i=1,2\) es:

\[C_i(q_i) = 0.5c_iq^2_i\]

Con esto es posible escribir la función de beneficios de la empresa \(i\) como:

\[\pi(q_1,q_2) = P(q_1+q_2)q_i - C_i(q_i)\]

Reemplazando tenemos:

\[\pi(q_1,q_2) = (q_1+q_2)^{1/\eta}q_i - 0.5c_iq^2_i\]

Cada firma busca maximizar su beneficio eligiendo la cantidad que produce y tomando como dada la decisión de la otra empresa.

Las condiciones de primer orden son:

\[(q_1+q_2)^{-1/\eta} - (1/\eta)(q_1+q_2)^{-1/\eta-1} - c_iq_i = 0, \ \ \ i=1,2\]

Note que el equilibrio está caracterizado por la solución del sistema de dos ecuaciones no lineales anterior.

Para resolver el modelo escribimos la siguiente función:

function cournot(q,c,eta)

    neq = length(q)
    fval = zeros(neq,1)

    q1 = q[1]
    q2 = q[2]

    c1 = c[1]
    c2 = c[2]

    fval[1] = (q1+q2)^(-1/eta) - (1/eta)*((q1+q2)^(-(1/eta)-1))*q1 - c1*q1
    fval[2] = (q1+q2)^(-1/eta) - (1/eta)*((q1+q2)^(-(1/eta)-1))*q2 - c2*q2
    
    return fval

end

cournot (generic function with 1 method)

Definimos los parámetros:

c = [0.6, 0.6]
eta = 1.2;

Usamos nlsolve para encontrar la solución:

using NLsolve

q0 = [0.2, 0.2]
sol_cournot = nlsolve(x -> cournot(x,c,eta), q0, inplace = false);

qstar = sol_cournot.zero

2-element Array{Float64,1}:
 0.7186126263887692
 0.7186126263887692

La idea de escribir la función dejando c y eta como inputs permite simular la solución bajo distintos niveles de costos y de la elasticidad de la demanda.

13.4 Estimación por Máximo Verosimilitud

Suponga que buscamos estimar el siguiente modelo de regresión lineal:

\[y_i = \beta_0 + \beta_1 x_{1i}+ \beta_2 x_{2i} + u_i\]

por el método de máximo verosimilitud. Para ello suponemos que:

\[u_i \sim N(0,\sigma^2)\]

Usaremos los datos que generamos para la aplicación sobre MCO.

using DelimitedFiles
using Distributions
using Optim

impdata = readdlm("DatosMCO.txt", ',')
N, K = size(impdata)
y = impdata[:,1]
X1 = impdata[:,2]
X2 = impdata[:,3]

X = [X1 X2]

100×2 Array{Float64,2}:
  2.0753    3.6808 
  4.6678    0.22394
 -3.5177    2.2002 
  2.7243    0.91094
  1.6375    2.607  
 -1.6154    0.79935
  0.13282   2.9799 
  1.6852    3.4787 
  8.1568    5.4238 
  6.5389    1.6118 
 -1.6998   -2.2767 
  7.0698    0.32082
  2.4508    4.7092 
  ⋮                
  1.4313    3.3203 
 -1.3317    1.8643 
 -1.2959    1.6096 
  1.2097    1.5648 
  2.4445    1.3938 
  6.171     2.0461 
 -0.33378   2.1026 
  1.3747    3.6521 
  0.83501   5.054  
 -2.866     2.9338 
  0.12207   1.5806 
 -2.5894    3.2504

La función de verosimilitud se define como:

\[L(y,x1,x2|\beta_0,\beta_1,\beta_2,\sigma) = \prod^n_{i=1} f(u_i)\]

donde \(f(u_i)\) es la función de densidad normal. Tomando logaritmos:

\[\ln L(y,x1,x2|\beta_0,\beta_1,\beta_2,\sigma) = \sum^n_{i=1} \ln f(u_i)\]

El objetivo es maximizar \[\ln L(y,x1,x2|\beta_0,\beta_1,\beta_2,\sigma)\] eligiendo los parámetros \((\beta_0,\beta_1,\beta_2,\sigma)\).

El primer paso es escribir la función de verosimilitud y para ellos haremos uso del paquete Distributions.

Maximizamos la función de verosimilitud:

function loglike(par,y,X)

    beta0 = par[1]
    beta1 = par[2]
    beta2 = par[3]
    sig   = exp(par[4])

    N = length(y)

    L = zeros(N)
    
    d = Normal(0,sig)

    for i in 1:N
        ui = y[i] - beta0 - beta1*X[i,1] - beta2*X[i,2]
        L[i] = pdf(d,ui)
    end
    # L = [pdf(d, y[i] - beta0 - beta1*X[i,1] - beta2*X[i,2]) for i in 1:N]    # Alternativa

    return -sum(log.(L))

end

loglike (generic function with 1 method)

par0 = [2, 0.1, 0.1, log(2)]
res_mv = optimize(x -> loglike(x,y,X), par0, LBFGS());

params = res_mv.minimizer

4-element Array{Float64,1}:
  2.9913098845479613  
  0.5639635070838799  
  0.8019684022883052  
 -0.016972951811933548

Los datos fueron generados bajo el siguiente modelo:

\[y_i = 3 + 0.5X_{1i} + 0.9X_{2i} + u_i\]

donde \(u_i \sim N(0,1)\).

Finalmente, la desviación estándar será:

sig = exp(params[4])

0.9831702772498274

13.5 El Problema de Maximización del Consumidor

Suponga que un consumidor busca maximizar la siguiente función de utilidad:

\[U(x_1,x_2,...,x_n) = \sum^{n}_{i=1}x^{\alpha_i}_i\]

con \(\sum^{n}_{i=1}\alpha_i = 1\). Sujeto a la restricción presupuestaria:

\[p_1x_1 + p_2x_2 + ... + p_nx_n \leq m\]

y las restricciones de no negatividad:

\[x_i \geq 0 \]

con \(m\) es ingreso y \(p_i\) el precio del bien \(i\).

Maximicemos la utilidad bajo el supuesto que existen 4 bienes. Definimos los parámetros del modelo:

using JuMP
using Ipopt

modelo_consumidor = Model(with_optimizer(Ipopt.Optimizer));

Ahora definimos los parámetros de optimización:

alpha = [0.2, 0.4, 0.1, 0.3]
p = [2, 3, 4, 5]
m = 100;

Declaramos las variables y sus restricciones individuales:

@variable(modelo_consumidor, 0 <= x[1:4])

4-element Array{VariableRef,1}:
 x[1]
 x[2]
 x[3]
 x[4]

Declaramos la restricción presupuestaria:

@constraint(modelo_consumidor, sum(x.*p) <= m)

Optimizamos:

# Note que definimos la función de utilidad como negativa para maximizar.
@NLobjective(modelo_consumidor, Min, -(x[1]^alpha[1] + x[2]^alpha[2] + x[3]^alpha[3] + x[4]^alpha[4]));

print(modelo_consumidor)

Min -((x[1] ^ 0.2 + x[2] ^ 0.4 + x[3] ^ 0.1 + x[4] ^ 0.3))
Subject to
 x[1] ≥ 0.0
 x[2] ≥ 0.0
 x[3] ≥ 0.0
 x[4] ≥ 0.0
 2 x[1] + 3 x[2] + 4 x[3] + 5 x[4] ≤ 100.0

optimize!(modelo_consumidor);

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
 Ipopt is released as open source code under the Eclipse Public License (EPL).
         For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************

This is Ipopt version 3.12.10, running with linear solver mumps.
NOTE: Other linear solvers might be more efficient (see Ipopt documentation).

Number of nonzeros in equality constraint Jacobian...:        0
Number of nonzeros in inequality constraint Jacobian.:        4
Number of nonzeros in Lagrangian Hessian.............:        4

Total number of variables............................:        4
                     variables with only lower bounds:        4
                variables with lower and upper bounds:        0
                     variables with only upper bounds:        0
Total number of equality constraints.................:        0
Total number of inequality constraints...............:        1
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        1

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0 -1.4387422e+00 0.00e+00 7.27e-01  -1.0 0.00e+00    -  0.00e+00 0.00e+00   0
   1 -2.3718229e+00 0.00e+00 1.57e-06  -1.0 1.39e+00    -  1.00e+00 1.00e+00f  1
   2 -4.8413909e+00 0.00e+00 1.27e-06  -1.0 2.63e+01    -  1.00e+00 1.00e+00f  1
   3 -5.2618784e+00 0.00e+00 2.00e-07  -1.7 1.04e+01    -  1.00e+00 1.00e+00f  1
   4 -5.4652038e+00 0.00e+00 2.83e-08  -2.5 5.91e+00    -  1.00e+00 1.00e+00f  1
   5 -5.5268237e+00 0.00e+00 1.51e-09  -3.8 1.91e+00    -  1.00e+00 1.00e+00f  1
   6 -5.5400961e+00 0.00e+00 1.85e-11  -5.7 4.17e-01    -  1.00e+00 1.00e+00h  1
   7 -5.5458621e+00 0.00e+00 1.59e-09  -8.6 1.31e-01    -  9.97e-01 1.00e+00h  1
   8 -6.4821779e+00 0.00e+00 7.46e-10  -8.6 2.44e+01    -  1.00e+00 1.00e+00h  1
   9 -6.9698162e+00 0.00e+00 3.38e-10 -12.9 1.57e+01    -  7.03e-01 1.00e+00h  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  10 -7.3376777e+00 0.00e+00 1.07e-10 -12.9 1.28e+01    -  9.82e-01 1.00e+00f  1
  11 -7.3514658e+00 0.00e+00 7.47e-12 -12.9 1.26e+00    -  1.00e+00 9.52e-01f  1
  12 -7.3514699e+00 0.00e+00 1.01e-11 -12.9 6.00e-02    -  1.00e+00 1.25e-01f  4

Number of Iterations....: 12

                                   (scaled)                 (unscaled)
Objective...............:  -7.3514699355951978e-08   -7.3514699355951976e+00
Dual infeasibility......:   1.0112796742107022e-11    1.0112796742107022e-03
Constraint violation....:   0.0000000000000000e+00    0.0000000000000000e+00
Complementarity.........:   5.8493693237061796e-13    5.8493693237061794e-05
Overall NLP error.......:   1.0112796742107022e-11    1.0112796742107022e-03


Number of objective function evaluations             = 16
Number of objective gradient evaluations             = 13
Number of equality constraint evaluations            = 0
Number of inequality constraint evaluations          = 16
Number of equality constraint Jacobian evaluations   = 0
Number of inequality constraint Jacobian evaluations = 1
Number of Lagrangian Hessian evaluations             = 12
Total CPU secs in IPOPT (w/o function evaluations)   =      3.212
Total CPU secs in NLP function evaluations           =      1.052

EXIT: Optimal Solution Found.

Las cantidades óptimas individuales son:

xstar = [JuMP.value(x[i]) for i in 1:4]
xstar

4-element Array{Float64,1}:
  6.694356521017993
 20.25055985182754 
  1.179533765726216
  4.228280457060584

Ahora definimos los parámetros de optimización:

sum(p.*xstar)

99.99992994572638